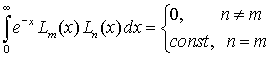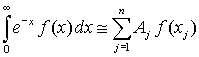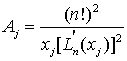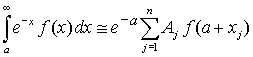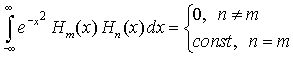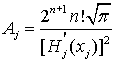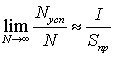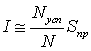|
ПРИБЛИЖЕННОЕ ВЫЧИСЛЕНИЕ ОПРЕДЕЛЕННЫХ ИНТЕГРАЛОВПри решении задач научного и инженерно-технического характера математическими методами часто возникает необходимость проинтегрировать какую-либо функцию. Есть функции, которые невозможно интегрировать аналитически, т.е. только в некоторых случаях по заданной функции можно найти первообразную. Общим способом интегрирования любых функций является численное интегрирование, методы которого в большинстве своем просты и легко переводятся на алгоритмические языки. Геометрически интеграл функции f(x) в пределах от a до b представляет собой площадь криволинейной трапеции, ограниченной графиком этой функции, осью x и прямыми x = a и x = b. Численные методы интегрирования используют замену площади криволинейной трапеции на конечную сумму площадей более простых геометрических фигур, которые могут быть вычислены точно. В этом смысле говорят об использовании квадратурных формул (по аналогии с задачей о квадратуре круга – построение квадрата с площадью, равной площади круга с определенным радиусом). В большинстве методов используется приближенной представление интеграла в виде конечной суммы (квадратурная формула):
где ci – постоянные, называемые весами, а xi – принадлежат интервалу [ a, b] и называются узлами. В основе квадратурных формул лежит идея аппроксимации на отрезке интегрирования графика подынтегрального выражения функциями более простого вида, которые легко могут быть проинтегрированы аналитически и, таким образом, легко вычислены. Наиболее просто задача построения квадратурных формул реализуется для полиномиальных математических моделей. Многочлен (полином) порядка n имеет вид
и определяется, таким образом, значениями (n+1)
констант ai . Если известно значение функции в
(n+1) точках
Если все xi различны, то данная система уравнений имеет единственное решение, так как определитель системы, составленный из коэффициентов системы линейных уравнений (так называемый определитель Вандермонда) будет отличен от нуля
Определив коэффициенты интерполяционного многочлена, можно легко вычислить приближенное значение интеграла, заменив подынтегральную функцию на полученный многочлен
Узлы интерполирования на отрезке интегрирования могут быть расположены на равном удалении друг от друга (эквидистантные узлы). В этом случае для полинома степени n имеем следующее
h – шаг, xi – узлы интерполирования. При n = 0 получаем метод прямоугольников. График функции f(x) на отрезке интегрирования заменяется на горизонтальную линию (полином степени 0).
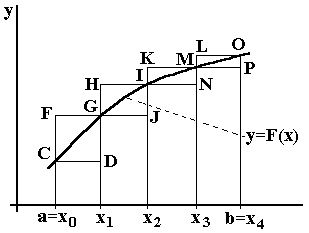
Интегрирование методом прямоугольников (метод Эйлера). Пусть функцию (рисунок справа ) необходимо проинтегрировать численным методом на отрезке [a, b]. Разделим отрезок на N равных интервалов (на рисунке N = 4). Площадь каждой из 4-х криволинейных трапеций можно заменить на площадь прямоугольника. Ширина всех прямоугольников одинакова и равна В качестве выбора высоты прямоугольников можно предложить выбрать значение функции на левой границе. В этом случае высота первого прямоугольника составит f(a), второго – f(x1), третьего – f(x2), последнего – f(x3). Приближенное значение интеграла получается суммированием площадей прямоугольников
Если в качестве выбора высоты прямоугольников взять значение функции на правой границе, то в этом случае высота первого прямоугольника составит f(x1), второго – f(x2), третьего – f(x3), последнего – f(b).
Как видно, в этом случае, одна из формул дает приближение к интегралу с избытком, а вторая c недостатком. Можно предложить еще один способ, очевидно лучший, чем обе эти формулы – использовать для аппроксимации значение функции в середине отрезка интегрирования.
В общем виде, если отрезок [a, b] разбить на N равных интервалов интегрирования (h) и к каждому интервалу применить формулу прямоугольников, то получим
Использование для интерполяции полинома первой степени (прямая линия, проведенная через две точки) приводит к формуле трапеций. В качестве узлов интерполирования берутся концы отрезка интегрирования. Таким образом, криволинейная трапеция заменяется на обычную трапецию, площадь которой может быть найдена как произведение полусуммы оснований на высоту.
В случае N отрезков интегрирования для всех узлов, за исключением крайних точек отрезка, значение функции войдет в общую сумму дважды (так как соседние трапеции имеют одну общую сторону).
Интересно, что формула трапеций может быть получена, если взять половину суммы формул прямоугольников по правому и левому краям отрезка
Проиллюстрируем использование формулы трапеций на примере рисунка 1
Величину I можно представить как сумму площадей трапеций (в данном случае четырех)
Проверка устойчивости решения Как правило, чем меньше длина каждого интервала, т.е. чем больше число этих интервалов, тем меньше различаются приближенное и точное значение интеграла. Это справедливо для большинства функций. В методе трапеций ошибка вычисления интеграла (δ) приблизительно пропорциональна квадрату шага интегрирования h 2 δ ~ h 2 Таким образом, для вычисления интеграла некоторой функции в пределах a, b необходимо разделить отрезок [a, b] на n0 интервалов и найти сумму площадей трапеций. Затем нужно увеличить число интервалов (n1), опять вычислить сумму трапеций и сравнить полученное значение с предыдущим результатом. Это следует повторять до тех пор (ni), пока не будет достигнута заданная точность результата (критерия сходимости). Для методов прямоугольников и трапеций обычно на каждом шаге итерации число интервалов увеличивается в 2 раза, т.е. ni+1 = 2 ni. Алгоритм процедуры интегрирования можно записать следующим образом: интеграл (I) рассчитывается по формуле
а критерий сходимости
Главное преимущество правила трапеций – его простота. Однако если при вычислении интеграла требуется высокая точность, применение этого метода может потребовать слишком большого количества итераций или машинного времени. Пример: Пользуясь правилом трапеций вычислить интеграл Для n = 1 Для n = 2 Для n = 4
Для n = 64 Использование трех точек для интерполирования подынтегрального выражения позволяет использовать параболическую функцию (полином второй степени). Это приводит к формуле Симпсона приближенного вычисления интеграла. Рассмотрим произвольный интеграл
Воспользуемся заменой переменной таким образом, чтобы границы отрезка интегрирования вместо [a,b] стали [-1,1], для этого введем переменную z:
Рассмотрим задачу интерполирования полиномом второй степени (параболой) подынтегральной функции, используя в качестве узлов три равноудаленные узловые точки –
Система уравнений для нахождения коэффициентов полинома
Примет вид
Коэффициенты легко могут быть получены
Вычислим теперь значение интеграла от интерполяционного многочлена
Путем обратной замены переменной вернемся к исходному интегралу. Учтем, что
Получим формулу Симпсона для произвольного интервала интегрирования: При необходимости, исходный отрезок интегрирования может быть разбит на N сдвоенных отрезков, к каждому из которых применяется формула Симпсона. Шаг интерполирования при этом составит
Для первого отрезка интегрирования узлами интерполирования будут являться точки a, a+h, a+2h, для второго – a+2h, a+3h, a+4h, третьего a+4h, a+5h, a+6h и т.д. Приближенное значение интеграла получается суммированием N площадей:
В данную сумму входят одинаковые слагаемые (для внутренних узлов с четным значением индекса - 2i). Поэтому можно перегруппировать слагаемые в этой сумме таким образом
Погрешность этого приближенного метода уменьшается пропорционально длине шага интегрирования в четвертой степени, т.е. при увеличении числа интервалов вдвое ошибка уменьшается в 16 раз δ ~ h 4 Пример: Пользуясь правилом Симпсона вычислить интеграл Для n = 1
Для n = 2
Правило Симпсона позволяет точно рассчитать интеграл не только от квадратичной функции, но и для полинома третей степени
Квадратуры Гаусса-Котеса. Числа Котеса Обобщением на случай равноточечной интерполяции полиномом степени n является квадратурная формула Гаусса-Котеса. Числа Котеса – это коэффициенты Aj (веса) в следующей формуле:
Индекс j используется для отличия от перечисленных выше итерационных методов. На каждом отрезке интегрирования подынтегральная функция аппроксимируется полиномом степени n (то есть используется n+1 узел). При выводе формул Гаусса-Котеса предполагается эквидистантность (равноточечность, равная удаленность) абсцисс узлов.
Числа Котеса
В таблице приведены коэффициенты первых восьми формул Котеса. Легко видеть, что при n = 1 и n = 2 формула Гаусса-Котеса полностью соответствует, соответственно, формуле трапеций и формуле Симпсона. В качестве примера рассмотрим семиточечный алгоритм (степень полинома n = 6):
Пример: Используя семиточечную формулу вычислить интеграл (Точное решение - 2,3201169227)
Абсолютная ошибка определения интеграла равна 5,3·10-9. Таким образом, использование данного алгоритма с числами Котеса при высоком точечном значении, позволяет находить за один шаг интегралы с достаточной степенью точности. [a, b] формулу алгоритма легко получить заменой переменной
Квадратурные формулы, полученные при равноточечном интерполировании подынтегрального выражения полиномом степени n, оказываются точными для нахождения интегралов где f(x) – это полиномиальная функция степени, меньшей и равной n (за исключенем n = 2, для которого точно вычисляется и интеграл от кубической функции). Максимальная степень полинома, для которой квадратурная формула является точной называется алгебраической мерой точности квадратуры. Можно получить квадратурные формулы с алгебраической точностью не хуже 2n-1 , если при интерполировании подынтегрального выражения оптимизировать положение узлов с целью более точного расчета интеграла при заданной степени аппроксимирующего полинома. При выводе квадратурных формул Гаусса-Кристоффеля свободными параметрами считаются абсциссы (узлы) точек интерполяции и множители Aj (то есть всего 2n параметр). Оптимизация по этим параметрам значительно увеличивает точность квадратурных формул, которые, в общем, имеют вид
где w(x) – весовая функция, Aj – веса, xj – узлы. n – это степень полинома, используемого для интерполяции подынтегрального выражения. Узлы интерполирования xj, что очевидно, должны лежать на отрезке интегрирования [a, b]. Для вычисления оптимального положения узлов находят корни полиномов специального вида, так называемых ортогональных полиномов. Если для определенных [a, b] и при любых целых m и l для семейства полиномов Qm(x) (m – степень полинома) выполняется условие
то говорят, что семейство полиномов Qm(x) ортогонально на отрезке [a,b] с весовой функцией w(x). Замечательным свойством ортогональных полиномов является то, что при любом положительном m они имеют ровно m простых (различных) действительных корней, причем все они лежат на отрезке ортогональности [a, b]. Кроме того, можно доказать, что наивысшая алгебраическая точность 2n-1 квадратурных формул достигается при расположении узлов интерполирования в точках, соответствующих корням ортогональных полиномов. Соответствующие веса Aj могут быть рассчитаны через систему линейных уравнений (определитель Вандермонда). Вот некоторые общие свойства весов: 1) Aj > 0 , 2) Ниже в таблице приведены пределы интегрирования [a, b], весовые функции w(x) для некоторых наиболее часто используемых ортогональных полиномов. Ортогональные полиномы
C точностью до нормирующего множителя
Приведем несколько полиномов Лежандра:
Для вычисления полиномов Лежандра можно использовать рекуррентное соотношение:
Эти полиномы ортогональны в интервале [-1, 1] с весовой функцией
Корни полинома Pn(x) действительные, различные (невырожденные) и находятся в интервале [-1, 1]. Квадратурная формула Гаусса-Лежандра по n точкам имеет вид
Узлы xj являются корнями полинома Pn(x), а соответствующие веса Aj определяются формулой
Квадратурная формула Гаусса-Лежандра, использующая n точек, дает точные значения интегралов для всех полиномов степени не выше 2n-1. Для произвольного интервала [a, b] уравнение переходит в формулу
Существуют таблицы, в которых приведены узлы и веса для значений n до 512, вычисленные с точностью до 30 значащих цифр. Для проверки устойчивости найденного значения интеграла можно выбрать следующий алгоритм: на первой стадии (итерации) вычисляется интеграл по выше приведенной формуле (например, шеститочечная формула). Затем отрезок [a, b] делится пополам и на каждом подинтервале опять используется шеститочечная формула. Полученные два интеграла складываются. Если относительное изменение интеграла больше величины допуска, то интервал делится на три части и вычисляются соответствующие интегралы. Процедура повторяется до тех пор, пока не выполнится критерий сходимости или число итераций не превысит допустимое максимальное значение. В таблице приведены веса и узлы для первых семи полиномов Лежандра
Полиномы Чебышева первого рода Эти полиномы также ортогональны в интервале [-1, 1] но с весовой функцией
Приведем несколько первых полиномов:
Tn(x) имеет вид
а квадратурная формула Гаусса-Чебышева
где
Для интервала [a, b] и произвольной функции G(z) квадратурная формула Гаусса-Чебышева имеет вид
где Примечание Действительно, сделав подстановку Получаем пределы интегрирования [-1, 1] и откуда легко получить записанное ранее выражение для интеграла. Полиномы Лагерра ортогональны в интервале [0, +∞] с весовой функцией
Приведем несколько полиномов Лагерра:
Полиномы Лагерра удовлетворяют рекуррентному соотношению:
Квадратурная формула Гаусса-Лагерра по n точкам имеет вид
где xj – корни полинома Ln(x) , а
Для интервала [a, +∞] квадратурная формула имеет вид
Существуют таблицы, в которых приведены узлы и веса с точностью до 30 значащих цифр вплоть до n = 68.
Полиномы Эрмита ортогональны в интервале [–∞,+∞] с весовой функцией
Приведем выражения для нескольких первых полиномов Эрмита:
Рекуррентное соотношение для полиномов Эрмита Hn(x) имеет вид
Узлы являются корнями Hn(x), а веса вычисляются по формуле
Существуют таблицы, в которых приведены узлы и веса с точностью до 30 значащих цифр вплоть до n = 136.
В некоторых случаях из-за особенности подынтегральной функции (например, из-за ее большой сложности, неявном способе задания и т.д.), описанные выше методы нельзя или нецелесообразно использовать. В задачах, не требующих высокой точности, широкое распространение получил метод Монте-Карло. Проиллюстрируем применение этого метода на примере приближенного вычисления следующего интеграла:
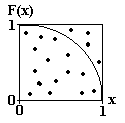
График подынтегрального выражения приведен на рисунке. Очевидно, что точное значение интеграла равно четверти площади круга единичного радиуса.
Иллюстрация метода Монте-Карло Построим прямоугольную область, которая будет полностью включать в себя искомый интеграл. В данном случае это будет квадрат с единичным ребром, показанный на рисунке. Далее, с помощью датчика случайных чисел генерируются точки
попадающие в эту область. В данном случае абсциссы и ординаты точек должны быть случайными числами, равномерно распределенными на отрезке [0, 1]. Для каждой точки проверяется, попадает ли она в область под или над графиком функции, то есть проверяется условие:
Если условие выполняется, то выбранная точка соответствует «успеху», если нет – то «промаху». Таким образом, процедура может быть описана как игра в «попадание» случайно выбранной точки в область под графиком (отсюда и название метода - Монте-Карло). Вполне очевидно, что отношение числа «попаданий» (Nусп) к общему числу попыток (N) должно в пределе стремиться к доли площади прямоугольной области (Sпр), которую занимает область под интегрируемой функцией (значение интеграла, I).
Отсюда получается формула метода Монте-Карло:
Для реализации метода существенное значение имеет качество используемого датчика случайных чисел. Идеальный датчик должен давать равномерное распределение чисел в заданном диапазоне. Точность расчета интеграла определяется так же числом точек (N), используемых при вычислениях и, очевидно, должна увеличиваться при его росте. Метод Монте-Карло широко используется в современных методах моделирования динамики молекулярных систем, взаимодействия растворенного вещества с молекулами растворителя, кинетики адсорбции веществ на твердых поверхностях и т.д. Пример. Вычислить объем молекулы, ограниченный Ван-дер-Ваальсовыми радиусами образующих ее атомов. Очевидно, что из рассмотренных методов единственно возможным является метод Монте-Карло. Подынтегральная функция в этом случае не имеет аналитического представления, зато достаточно легко можно проверить, попадает ли точка с произвольными координатами |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
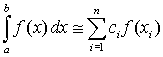
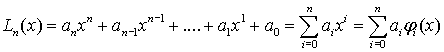 ,
, 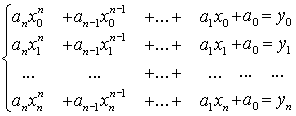
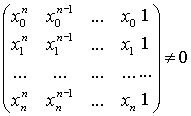
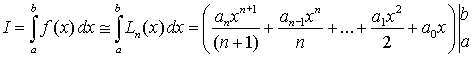
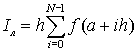
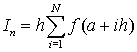
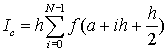
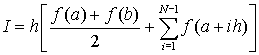
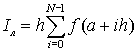
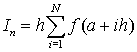
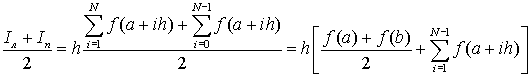
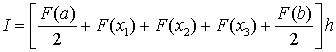
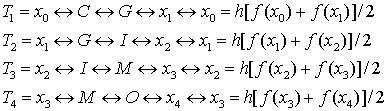
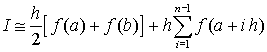 , где
, где 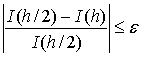
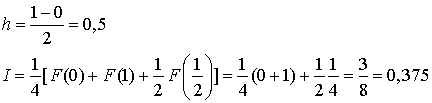
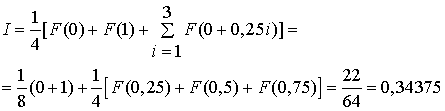
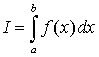
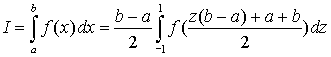
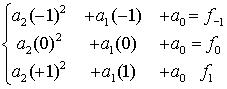 или
или 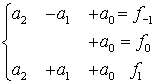
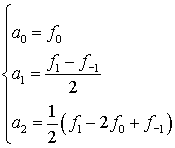
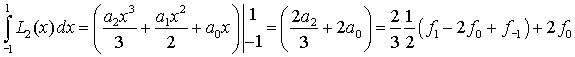
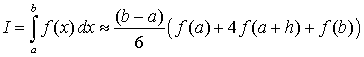 , и
, и 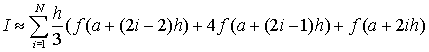
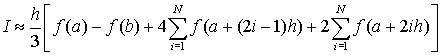 , что эквивалентно
, что эквивалентно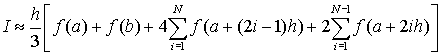 , так как
, так как 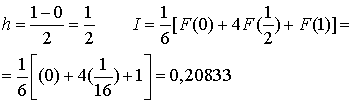
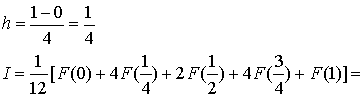
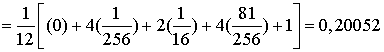
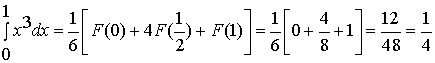
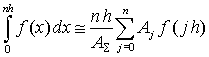
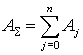
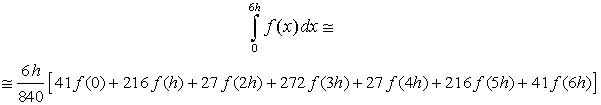
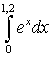 .
. 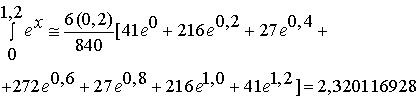
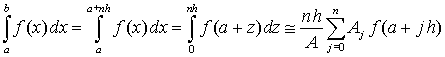 ,
, 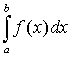 ,
, 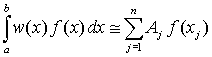
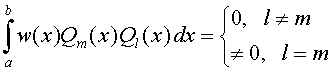 ,
,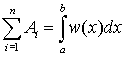
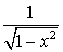
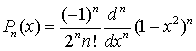
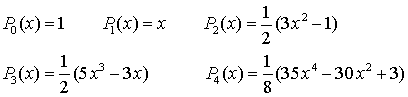
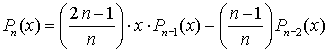
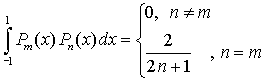
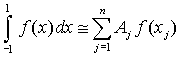
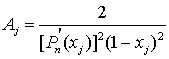
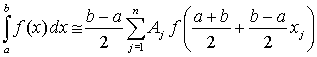
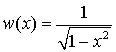 , т.е.
, т.е.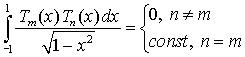
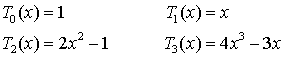
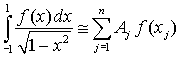
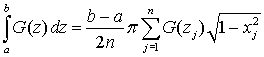
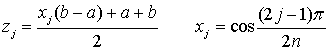
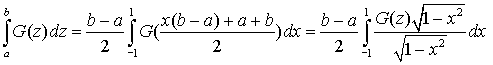 ,
,